Convex Polygons: Definition – Examples and Properties  

All polygons is either convex or concave. A polygon will be convex or concave, it depends on the measure of their angles. If the measures of all interior angles is less 180⁰ than the polygon is convex, otherwise the polygon is concave.

                        Convex Polygons 

Definition: If all the interior angles of a polygon is must be less than 180º, then it is called a convex polygon.

In a convex polygon, no diagonals goes outside of the figure, each diagonal lying inside or on the boundary of the polygon. It always lies in the polygon’s interior portion.

Examples of convex polygons:

In above figure there are four interior angles in rectangle ABCD, they are ∠A, ∠B, ∠C and ∠D. None of the four angles is not greater than 180ºevery angle is less than 180º.

The diagonals of rectangle ABCD,  AC and BD lies in the interior of the rectangle ABCD. So rectangle ABCD is a convex polygon.

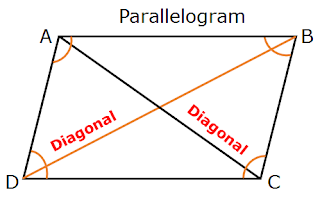
There are four interior angles in parallelogram ABCD, they are ∠A, ∠B, ∠C and ∠D. None of the four angle is not greater than 180º every angle is less than 180º.

The diagonals of parallelogram ABCD,  AC and BD lies in the interior of the parallelogram ABCD. So parallelogram ABCD is a convex polygon. 

        

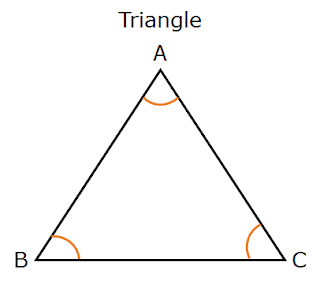
There are three interior angles in triangle ABC, they are ∠A, ∠B, and ∠C. None of the three angles is not greater than 180º every angle is less than 180º.

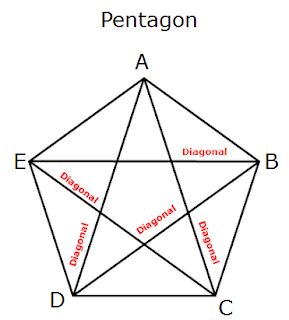
There are five interior angles in pentagon ABCDE, they are ∠A, ∠B, ∠C, ∠D and ∠E. None of the five angles not greater than every angle is less than 180º.

The diagonals of pentagon ABCDE, AC, AD, BE, EC and BD lies in the interior of the pentagon ABCDE. So pentagon ABCDE is a convex polygon.

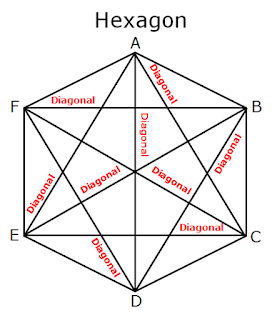
There are six interior angles in hexagon ABCDEF, they are ∠A, ∠B, ∠C, ∠D ∠E and ∠F. None of the six angles not greater than 180º every angle is less than 180º.

The diagonals of hexagon AE, AC, AD, EC, FC, FB, FD, BD, and BE lies in the interior of the hexagon ABCDEF. So hexagon ABCDEF is a convex polygon.

              Properties of a convex polygon

1. All the interior angles of a polygon is less than 180⁰.

2. A convex polygon have no angle inside which measure is greater than 180º.

3. In a convex polygon no diagonals goes to outside of the figure.

4. Another property of a convex polygon is a line segment joining any two points in the interior lies completely in the interior portion.