Converse of Pythagorean Theorem 

In this section we are going to see the converse of Pythagorean theorem.

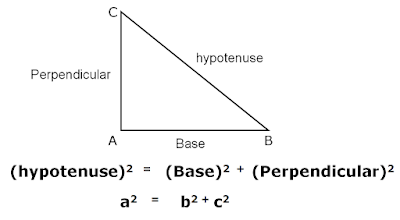
We know the Pythagorean theorem applies to right triangles and states that, 

The square of the length of the hypotenuse, equals the sum of the squares of the lengths of the other two sides. 

(hypotenuse)² = (Base)²+(Perpendicular)²

                                     a^{2    =}    b^2 + c²

The Converse of Pythagorean Theorem states that,

In a triangle, if the square of the length of one side is equal to the sum of the squares of the other two sides, then the angle opposite to the first side is a right angle.

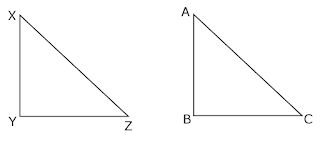
Given:  A △ XYZ in which

    XZ² = XY² + YZ²

To prove: ∠Y =  90⁰

Construction: Draw a △ ABC, such that,
      XY = AB,  YZ = BC,  and ∠B =  90⁰

So, by Pythagoras theorem we get,                         

AC² = XY² + YZ^2 …..(1) 

               (∵ XY = AB and YZ = BC)

But,  XZ² = XY² + YZ² ……(2) given

From (1) and (2) we get

                  XZ² = AC²
                  ∴ XZ = AC

Now in △ XYZ and △ ABC,

we get, XY = AB,  YZ = BC, and XZ = AC

Therefore, △ XYZ ≅ △ ABC

Hence, ∠Y = ∠B =  90⁰                   

 ∴ ∠Y =  90⁰  Proved

 Converse of Pythagorean Theorem -Word Problems

Example 1: Check whether a triangle with sides length are 3 cm, 5 cm, and 4 cm is a right triangle.

Solution:

We Check whether the square of the length of the longest side is the sum of the squares of the other two sides by the, converse of the Pythagorean theorem, the triangle is a right angle.

We know that the hypotenuse is the longest side in a triangle. 

If 3 cm., 5 cm,. and  4 cm. are the length of sides of the triangle, and 5 cm, is the longest side of the triangle then 5 cm. will be the hypotenuse.

Apply the converse of Pythagorean theorem, the square of the length of the longest side is sum of the squares of the other two sides.

                           5² = 4² + 3²

                           25 = 16 + 9

                           25 = 25

Since the square of the length of the longest side is the sum of the squares of the other two sides, by 
the, converse of the Pythagorean theorem, the triangle is a right angle.

Example 2: Check whether a triangle with sides length 8 cm, 6 cm, and 10 cm is a right triangle.

Solution:

We Check whether the square of the length of the longest side is the sum of the squares of the other two sides by the, converse of the Pythagorean theorem, the triangle is a right angle.

We know that the hypotenuse is the longest side in a triangle. 

If 3 cm., 5 cm,. and  4 cm. are the length of sides of the triangle, and 5 cm, is the longest side of the triangle then 5 cm. will be the hypotenuse.
Apply the converse of Pythagorean theorem, the square of the length of the longest side is sum of the squares of the other two sides.

                           10² = 8² + 6²

                           100 = 64 + 36

                           100 = 100

Since the square of the length of the longest side is the sum of the squares of the other two sides.
by the, converse of the Pythagorean theorem, the triangle is a right angle.

In a triangle with side lengths are a, b, and c, where c is the length of the longest side,

if  c^{2 <} a² + b² then the triangle is an acute triangle and
if  c² > a² + b²then the triangle is obtuse triangle.

Example 3: Check whether the triangle with side lengths are 5, 9, and 7 units is an acute, obtuse or right triangle.

Solution: The length of the longest side of the triangle is 9 units.

Other two sides of the triangle are 5 units and 7 units.

Now compare the square of the length of longest side and the sum of squares of the other two sides.

Square of the length of the longest side is 9² = 81 square units

Sum of squares of the other two sides is = 5² + 7²

                     5² + 7²   =  25 + 49 

                                  = 74 square units.

                             81 > 74

                     ∴     9²  > 5² + 7²

Therefore, the corollary to the the converse of the Pythagorean theorem, the triangle is an obtuse triangle.

Example 4. The length of sides of a triangle are 6 cm, 7.5 cm, and 4.5 cm. Is an acute, obtuse or right 
triangle. If the triangle is right triangle, which side is the hypotenuse? 

Solution: We know that in a right triangle the hypotenuse is the longest side. If 6 cm, 7.5 cm and 4.5 cm are the lengths of triangle, then 7.5 will be the hypotenuse.

Using the converse of Pythagorean theorem, we get

                        7.5² = 4.5² + 6²

                      56.25 = 36 + 20.25 

                                      = 56.25

                             56.25 = 56.25

Since both sides are equal therefore, 6 cm, 7.5 cm, and 4.5 cm are the sides of the right angled triangle and hypotenuse will be the 7.5 cm.

Example 5. The lengths of sides of a triangle are 5 cm, 10 cm, and 15 cm. Is an an acute, obtuse or right triangle. If the triangle is right triangle, which side is the hypotenuse?

Solution: We know that in a right triangle the hypotenuse is the longest side. If 5 cm, 10 cm and 15 cm are the lengths of triangle, then 15 will be the hypotenuse.

Using the converse of Pythagorean theorem, we get

                           15² = 5² + 10²

                          225 = 100 + 25 

                                 = 125   

                               225 ≠ 125

                               225 > 125

                     ∴     15²  > 5² + 10²

Since both sides are not equal therefore, 5 cm, 10 cm, and 15 cm are not the sides of the right angled triangle.

Therefore, the corollary to the the converse of the Pythagorean theorem, the triangle is an obtuse triangle.

Example 6. The lengths of sides of a triangle are 8 cm, 15 cm, and 17 cm. Is an an acute, obtuse or right triangle. If the triangle is right triangle, which side is the hypotenuse? 

Solution: We know that, in a right triangle the hypotenuse is the longest side. If 8 cm, 15 cm and 17 cm are the lengths of triangle, then 17 will be the hypotenuse.

Using the converse of Pythagoras theorem, we get,

                        17²  = 15² + 8²

                        289 = 64 + 225 

                         289 = 289

Since both sides are equal therefore, 8 cm., 15 cm., and 17 cm. are the sides of the right angled triangle and hypotenuse will be the 17 cm.

Example 7. The lengths of sides of a triangle are 6 cm, 5 cm, and 11 cm. Is an an acute, obtuse or right 
triangle. If the triangle is right triangle, which side is the hypotenuse? 

Solution: We know that in a right triangle the hypotenuse is the longest side. If 6 cm, 5 cm and 11 cm are the lengths of triangle, then 11 will be the hypotenuse.

Using the converse of Pythagoras theorem theorem, we get,
                           11²  = 5² + 6²

                         121 = 36 + 25 

                                = 61

                             121 ≠ 61

                              121 > 61

Since both sides are not equal therefore, 6 cm, 5 cm, and 11 cm are not the sides of the right angled triangle. The triangle is an obtuse triangle.

If the lengths of the sides of the triangle will be given in the questions then the above examples of the 
converse of Pythagorean theorem will help us to determine the right triangle.

If the square of the length of the longest side is the sum of the squares of the other two sides by the, 
converse of the Pythagorean theorem, the triangle is a right angle.

If the square of length of one side of a triangle is equal to the sum of the squares of the other two sides, then the angle opposite to the first side is a right angle.

of the length of one side of a triangle is equal to the sum of the squares of the other two sides, then the angle opposite to the first side is a right angle.

Example 8. The side of a triangle are of length 9 cm, 11 cm and 6 cm. Is this triangle a right triangle? If so, which side is the hypotenuse?

Solution: We know that hypotenuse is the longest side. If 9 cm, 11 cm and 6 cm are the lengths of angled triangle, then 11 cm will be the hypotenuse.

Using the converse of Pythagorean theorem, we get,

11²  = 6² + 9²

                           121 = 36 + 81 

                            121 = 117

                            121 ≠ 117

                             121 > 117

Since both sides are not equal therefore, 11 cm, 6 cm, and 9 cm are not the sides of the right angled triangle. The triangle is an obtuse triangle.

Since, both the sides are not equal therefore 9 cm, 11 cm and 6 cm are not the side of the right angled 
triangle.

The above examples of the converse of Pythagorean Theorem will help us to determine the right triangle when the sides of the triangles will be given in the questions.

If the square of the length of the longest side of a triangle is equal to the sum of the squares of the other two sides, then the triangle is a right triangle.

The length of one side of a triangle is equal to the sum of the squares of the other two sides, then the angle opposite to the first side is a right angle.