Property of Integers – Additive Identity

What is Additive Identity Property

The additive identity property is one of the important property of addition of numbers.

Addition is process to bring two or more numbers together and make a new number.

Thus, if we add zero to any number the result will be the same number.

The additive property states that the sum of any number and 0 is the number itself.

When we add 0 to any number, it does not change the number.

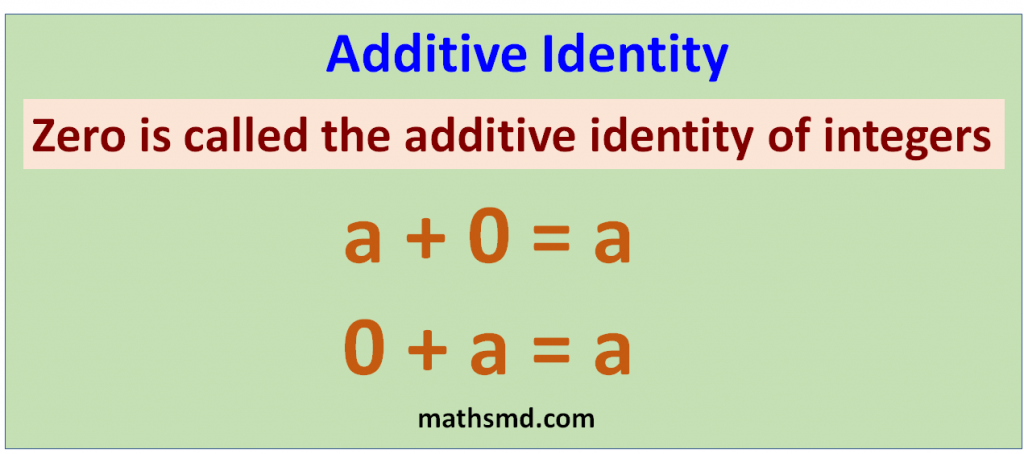
Zero is called additive identity for integers.

or

Additive Property states that when zero is added to any integer, it will give the same given number.

When we add zero to any integer, we get the same integer.

The additive identity property is also called the identity property of zero.

For any integer a, a + 0 = a

This property is applicable in complex numbers, real numbers, rational numbers, integers etc.

Additive Identity Formula

The formula of additive property is

a + 0 = a

For any integer a + 0 = a = a + 0

This shows that when any number is added to zero, the result is number itself.

Therefore, zero is the additive identity for integers.

Example: 25 + 0 = 25, 92 + 0 = 92

Example: If we add 3 to 0 we get 3 as the result.

3 + 0 = 0

7 + 0 = 7 (Positive Integers)

-7 + 0 = -7 (Negative Integers)

5/2 + 0 = 5/2 (Fractions)

0.8 + 0 = 0.8 (Decimals)

p + 0 = p (Algebraic expansion)