Theorem – If the diagonals of a Quadrilateral bisect each other then that Quadrilateral is a Parallelogram
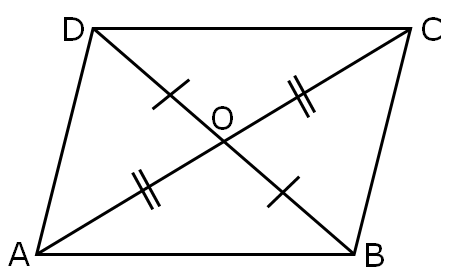
If the diagonals of a Quadrilateral, bisect each other then that Quadrilateral is a Parallelogram
Given: ABCD is a quadrilateral with AC and BD are diagonals and diagonals intersect each other at O.
i.e. OA = OC and OB = OD
To Prove: ABCD is a parallelogram.
Proof: In △AOD and △COB
OA = OC (Given)
OD = OB (Given)
∠AOD = ∠COB (Vertically opposite angles)
∴ △AOD ≅ △COB, (By SAS Congruence rule)
∴ ∠OAD = ∠OCB (CPCT)…..(1) Similarly, we can prove
△AOB ≅ △COD, (By SAS Congruence rule)
∴ ∠ABO = ∠CDO (CPCT)…….(2)
For lines AB and CD with transversal BD,
∠ABO and ∠CDO are alternate angles and are equal.
∴ Lines AB and CD are parallel i.e. AB ∥ CD.
For lines AD and BC with transversal AC,
∠OAD and ∠OCB are alternate angles and are equal.
∴ Lines AD and BC are parallel i.e. AD ∥ BC
Thus, in ABCD, both pairs of opposite sides are parallel.
∴ ABCD is a parallelogram.

