Hexagon – Definition – Shapes – Types – Formula – Properties

What is a Hexagon?

A hexagon is a six-sided polygon with various properties and types.

The word “hexagon” comes from the Greek words “hex,” meaning six, and “gonia,” meaning angle.

Here’s a detailed breakdown:

Definition

A hexagon is a polygon with six edges (sides) and six vertices (corners).

The simplest and most symmetrical type of hexagon is the regular hexagon, where all sides and angles are equal.

Shapes

Hexagons can be regular or irregular:

1. Regular Hexagon: All six sides and angles are equal. Each interior angle is 120°.
2. Irregular Hexagon: The sides and angles are not equal.

Types of Hexagons

1. Convex Hexagon: All interior angles are less than 180°, and no sides are inward.
2. Concave Hexagon: At least one interior angle is greater than 180°, and at least one side is inward.

Formulas

For a regular hexagon, the following formulas apply:

Perimeter (P): The perimeter is the sum of all sides.

P=6s

where s is the length of one side.

Area (A): The area of a regular hexagon can be calculated using the formula:

A={(3✓3)/2} ​​s²

where s is the length of one side.

Apothem (a): The apothem is the distance from the center to the midpoint of a side.

a=(s✓3)/2​​

Properties

Number of sides: 6

Number of vertices: 6

Sum of interior angles:

(n−2)×180º=720º

where n is the number of sides (6 for a hexagon).

Each interior angle in a regular hexagon:

720º/6=120º

Each exterior angle:

360º÷6=60º

Diagonals:

The number of diagonals in a hexagon can be calculated using the formula:

Number of diagonals=n(n−3)/2}

For a hexagon:

Number of diagonals=6(6−3)/2=9

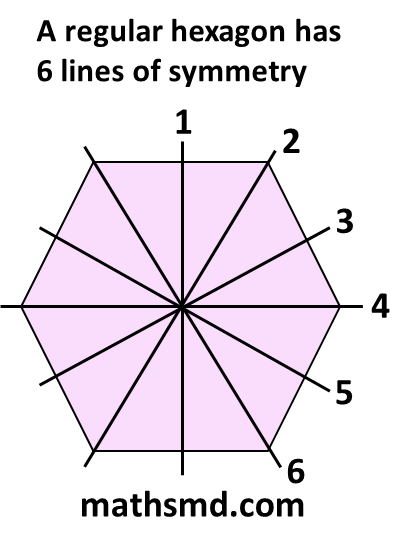
Symmetry:

A regular hexagon has 6 lines of symmetry.

It also has rotational symmetry of order 6 (i.e., it looks the same after a rotation of 60º or any multiple of 60º.

Examples

1. Regular Hexagon: Imagine a perfectly shaped honeycomb cell in a beehive. It has six equal sides and six equal angles, each measuring 120°.
2. Irregular Hexagon: Consider a playground area shaped with six sides, but not all sides or angles are equal.
3. Convex Hexagon: A common example is a regular hexagon, like the tiles often seen in bathroom or kitchen floors.
4. Concave Hexagon: Imagine a star-shaped figure with six sides where at least one angle is greater than 180°.

Example Calculation

Let’s calculate the area of a regular hexagon with a side length of 4 units.

Perimeter:

P=6s=6×4=24 units

Area:

A={(3✓3)/2}s²={(3✓3)/2}×4²=(3✓3/2}×16=24✓3

≈41.57 square units

Apothem:

a=s✓3/2=4√3/2=2√3≈3.46 units

Applications and Examples

• Nature: Hexagonal patterns are commonly found in nature, such as in honeycombs and certain crystals.
• Engineering and Architecture: Hexagonal shapes are used in tiling, design, and structural engineering due to their efficiency and strength.
• Games and Puzzles: Many board games and puzzles use hexagonal tiles or grids.
• Mathematics and Geometry: Hexagons are studied for their unique properties and relationships with other geometric shapes.

Summary

A hexagon is a six-sided polygon with a variety of interesting properties and applications. Regular hexagons, with their equal sides and angles, exhibit symmetrical characteristics that make them prevalent in both nature and human design. Understanding hexagons provides insight into more complex geometric concepts and their practical uses.

This breakdown covers the fundamental aspects of hexagons, including definitions, types, formulas, properties, and examples.