Rational Numbers – Multiplication

In this tutorial, we will learn, multiplication of rational numbers.

Multiplication of two rational numbers is just like multiplication of two integers. Product of two or more rational numbers is founded by multiplying the corresponding numerators and denominators of the numbers and writing them in the standard form.

Product of numerators divided by product of denominators is equal to multiplication of two rational Numbers.

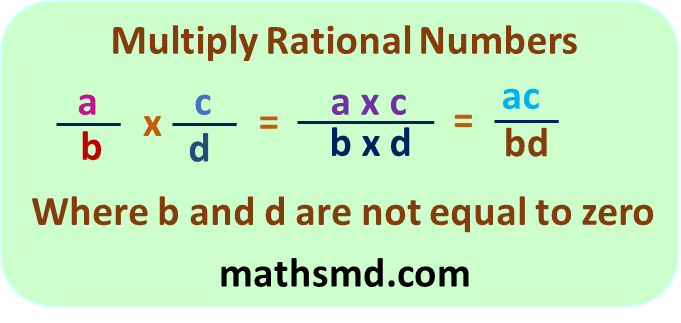
A rational number has integer values in numerator and denominator(denominator is not zero)

Product of rational numbers = Product of Numerators/ Product of Denominators

Example: (i) 3/4 x 7/5 = (3 x 7)/(4 x 5) = 21/20

(ii) 2/3 x 6/9 = (2 x 6)/(3 x 9) = 12/27 = 4/9

(iii) 4/5 x 3/8 = (4 x 3)/(5 x 8) = 12/40 = 3/10

(iv) -4/5 x 3/8 = (-4 x 3)/(5 x 8) = -12/40 = -3/10

(v) -4/5 x -3/8 = (-4 x -3)/(5 x 8) = 12/40 = 3/10

(vi) 4/5 x -3/8 = (4 x -3)/(5 x 8) = -12/40 = -3/10

(vii) 7/3 x -5/2 = (7 x -5)/(3 x 2) = -35/6

(viii) 7/3 x -3/7 = (7 x -3)/(3 x 7) = -1/1

If 0 is multiplied any rational number the result is always zero.

(i) 0 x 9/5 = (0 x 9)/5 = 0/5 = 0

(ii) 0 x -9/5 = (0 x -9)/5 = 0/5 = 0

(iii) 0 x -7/3 = 0

(iv) 0 x 5/1 = 0

When multiplying two rational numbers, we get the result as a rational number,

If ab and c are two rational numbers,

then ab x c = abc so (multiplication is closure)

If a and b are two rational numbers, then

a x b = b x a

ab = ba (multiplication is commutative)

If a, b and c are three rational numbers, then

a x (b x c) = (a x b) x c

abc = abc (multiplication is associative) for rational numbers.