Equation of a Circle When Center is Origin
Equation of a Circle when the Center of Circle Coincides with the Origin
In this tutorial we will learn, equation of a circle when the center of circle coincides with the origin with examples.
The equation of a circle in a Cartesian coordinate system can be expressed in a simple form when the center of the circle is at the origin (0, 0).
To understand this equation, let’s delve into the geometric and algebraic details.
Geometric Definition
A circle is the set of all points in a plane that are at a fixed distance (called the radius) from a fixed point (called the center). When the center is at the origin, this simplifies our calculations.
Derivation of the Equation
(1) Consider a point (x, y) on the circle.
(2) The distance between this point and the origin (0, 0) is equal to the radius r.
Using the distance formula between two points
(x1, y1) and (x2, y2):
Distance = ✓{(x2−x1)2 + (y2−y1)2}
For our circle, the distance from the origin (0, 0) to the point (x, y ) is the radius
r=✓{(x−0)2+(y−0)2}
Simplifying this, we get:
r= ✓(x2+y2)
Squaring Both Sides
To remove the square root, we square both sides of the equation:
r2 = x2 + y2
This is the standard form of the equation of a circle with center at the origin and radius r.
Summary of the Equation
The equation of a circle with center at the origin
(0,0) and radius r is:
x2 + y2 = r2
Examples
Circle with Radius 1:
If r=1, the equation becomes:
x2 + y2 = 1
Circle with Radius 5: If r=5,
x2 + y2 = 25
Graphical Representation
In the Cartesian plane, the equation
x2 + y2 = r2 represents a circle centered at the origin.
Every point (x,y) that satisfies this equation lies exactly r units away from the origin.
Key Points to Remember
The equation is symmetric about both the x-axis and y-axis.
The radius r is always a positive real number.
If r=0, the equation represents a degenerate circle which is just a point at the origin.
Equation of a circle with center at (h, k) and radius equal to r, is
(x – h)² + (y – k)² = r²……(1)
When the center of the circle(h, k) is (0, 0), coincides with the origin so, h = 0 and k = 0.
Putting the value in eq.(1)
(x – h)² + (y – k)² = r²
(x – 0)² + (y – 0)² = r²
Hence required equation of the circle is x² + y² = r².
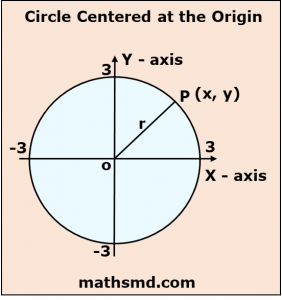
Consider an arbitrary point P(x, y) on a circle. Let ‘r’ be the radius of the circle which equal to OP.
We know that the distance between the point (x, y) and origin (0, 0) can be found using distance formula which is equal to √(x² + y²) = r.
Therefore, the equation of a circle, with the center as origin is x² + y² = r².
Alternative Method
Let (x, y) is a point on a circle and the center of the circle is at origin (0, 0).
Now we draw a perpendicular from point (x, y) to the x-axis, then we get a right angle triangle. In this right angle triangle radius of the circle is the hypotenuse.
The base of the triangle is the distance along x-axis and height is the distance along the y-axis.
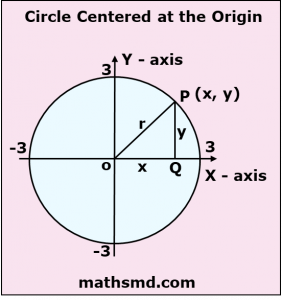
Thus applying the Pythagoras theorem, we get
x² + y² = r²
Equation of a circle when the center is origin is x² + y² = r²
Example: Find the equation of the circle whose center coincides with the origin and radius is 4 cm.
Solution: The equation of a circle whose center coincides with the origin and radius is 4 cm is
x² + y² = r²
x² + y² = 4²
x² + y² – 16 = 0
Example: Find the equation of the circle whose center coincides with the origin and radius is 2 cm.
Solution: The equation of a circle whose center coincides with the origin and radius is 2 cm is
x² + y² = r²
x² + y² = 2²
x² + y² = 4
x² + y² – 4 = 0
Example: Find the equation of the circle whose center coincides with the origin and radius is 9 cm.
Solution: The equation of a circle whose center coincides with the origin and radius is 9 cm is
x² + y² = r²
x² + y² = 9²
x² + y² = 81
x² + y² – 81 = 0
Conclusion
Understanding the equation of a circle with its center at the origin simplifies many problems in geometry and algebra. This foundational concept is crucial for more advanced studies in mathematics and its applications in various fields such as physics, engineering, and computer graphics.