Equation of a Circle when Center is not Origin

Equation of the circle when center is not origin.

Let P (x, y) are the cartesian coordinate of points on the circle, and (h, k) are the cartesian coordinate of the center of the circle, which is not the origin.

Therefore, OP is the radius of the circle.

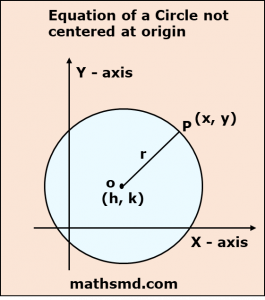
The radius of the circle is OP.

By using distance formula,

(x – h)² + (y – k) ² = OP ²

Let radius of the circle is r.

Therefore, the equation of the circle with center (h, k) and radius r is

(x – h)² + (y – k)² = r²

Equation of the circle with center (3, 2) and radius 5 is

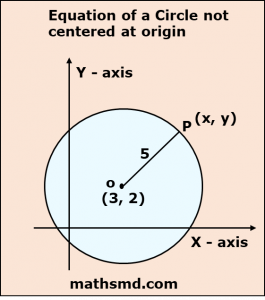
(x – h)² + (y – k)² = r²

(x – 3)² + (y – 2)² = 5²

(x – 3)² + (y – 2)² = 25