Corresponding Angles – Definition – Examples

Two angles that are corresponding are those that are located on the same side of a transversal in identical relative position. They typically result from a transversal cutting two lines, whether they are parallel or not.

In other words corresponding angles formed when a transversal line cuts across two straight lines.

If a transversal or a line crosses any two given parallel lines, then the corresponding angles formed have equal measure.

Definition:

Corresponding angles are angles that are formed when two parallel or non-parallel lines are intersected by the transversal.

When two lines are intersected by a transversal, two angles which occupy the same relative position at intersection are called corresponding angles.

Corresponding angles are equal, if the transversal intersects two parallel lines.

If the transversal intersects non-parallel lines, the corresponding angles formed are not congruent.

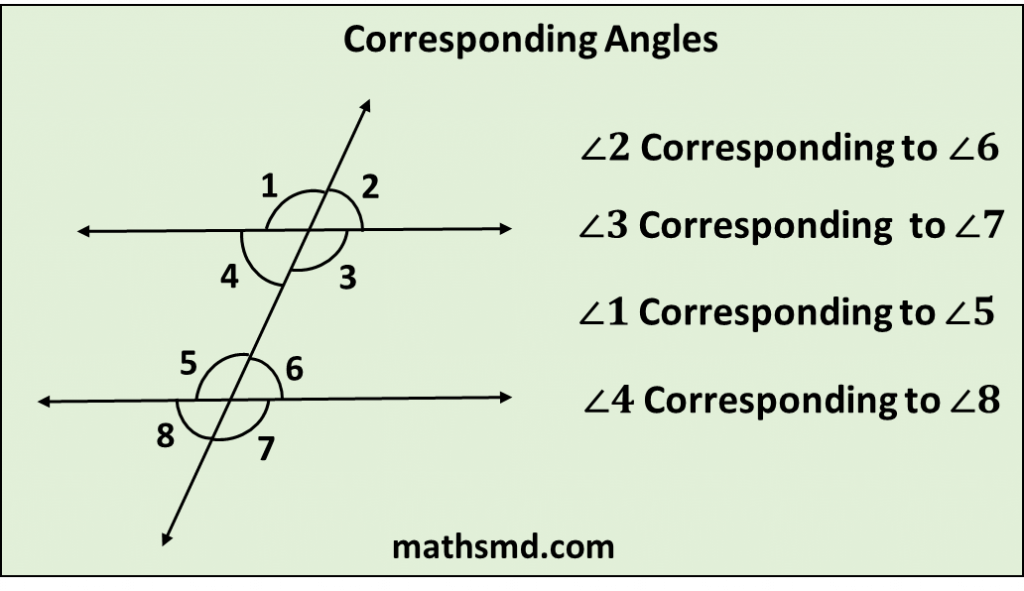
In the given figure, we can see the two parallel lines are intersected by a transversal, which forms eight angles with the transversal.

So, the angles formed by the first line with transversal have equal to the corresponding angles formed by the second line with transversal.

Name of Angles Location

Angles 1 and 5 Upper Right Side Angle

Angles 2 and 6 Upper Left Side

Angle Angles 3 and 7 Lower Right Side

Angle Angles 4 and 8 Lower Left Side Angle

If a transversal intersects non-parallel lines then the corresponding angles formed doesn’t have any relation with each other.

They are not equal as in the case of non-parallel lines but all are corresponding to each other.

Corresponding Angles Examples and Types

Examples of corresponding angles

Transversal can intersect either two parallel lines or two non-parallel lines. Thus, corresponding angles can be two types

(1) Corresponding angles formed by parallel lines and transversals.

(2) Corresponding angles formed by non-parallel lines and transversals.

Important notes on corresponding angles

(1) A pair of corresponding angles lie on the same side of the transversal.

(2) Corresponding angles are equal, if the transversal intersects two parallel lines.

(3) If the transversal intersects non-parallel lines, the corresponding angles formed are not congruent.

(4) Corresponding angles form are supplementary angles if the transversal perpendicularly intersects two parallel lines.

(5) If the lines are parallel interior angles on the same side of the transversal are supplementary.

(6) Similarly exterior angles are supplementary if the two line are parallel.