Exponents and Power Examples – Rules
Exponents and Power Rules
In this chapter we will learn about exponent and power.
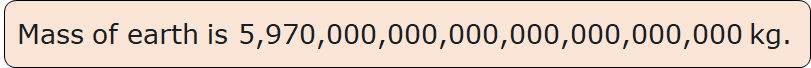

These are very large numbers, and difficult to read,
and compare.
To make these numbers easy to read, compare and understand we use exponents.
Exponents
Definition:
When a number repeatedly multiply by itself, we raise it to a power. This is known as Exponent.
or simply
An exponent is a number says, how many times a number is multiplied by itself.
Example: The expression 2³ is represents 2 x 2 x 2, which is equal to
2³ = 2 x 2 x 2 = 8
In words “2 to the power 3” or “2 cubed” or “cube of 2”.
“2” is called the base and “3” is exponent.
Exponents represents repeated multiplication.
Note: 2³ is not equal to 2 x 3 = 6
Example: The expression a4 is represents a x a x a x a. We cannot find the value of the expression without knowing the value of a.
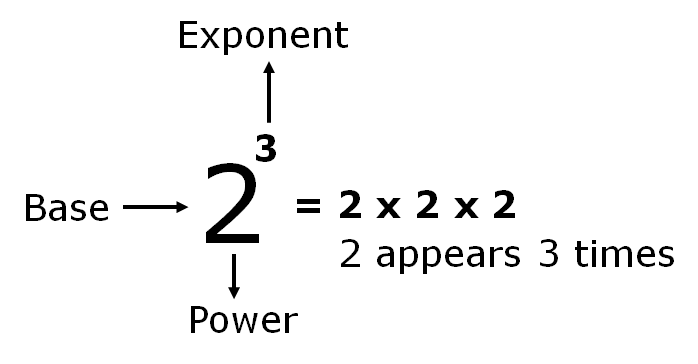
102 = 10 x 10, is called ten to the power 2, and read as “10 squared” or square of 10.
52 five to the power 2 is also read as “5 squared”.
10³ = 10 x 10 x10, is called “ten to the power 3” and read as “10 cubed” or “cube of 10 “10 to the third power”.
12³ twelve to the power 3 is also read as 12 cubed or cube of 12.
7³ is 7 to the power 3 is also read as 7 cubed or cube of 7.
104 is “10 to the fourth power” 10 to the power 4 or “10 to the 4.
Type of powers – Squares and cubes
| 1² = 1 | 2² = 4 | 3²=9 |
| 4² = 16 | 5² = 25 | 6² = 36 |
| 7² = 49 | 8² = 64 | 9² = 81 |
| 1³ = 1 | 2³ = 8 | 3³ = 27 |
| 4³ = 64 | 5³ = 125 | 6³ = 216 |
| 7³ = 343 | 8³ = 512 | 9³ = 729 |
Special Cases
(i) Any non zero number raised to the zero power equal to one.
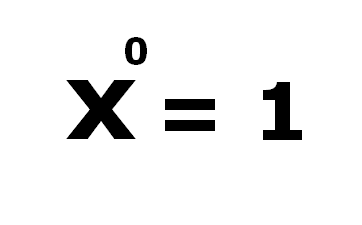
1° = 1
2° = 1
3° = 1
4° = 1
(ii) Raising any number to the power one gives back the same number.
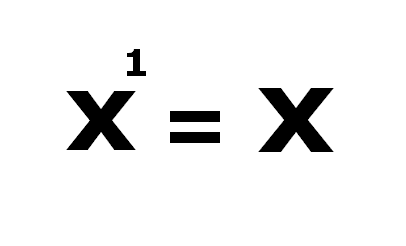
When x is any number other than 0.
1¹ = 1
2¹ = 2
3¹ = 3
4¹ = 4
The expression 3 x 3 is written in a short form 3 x 3 = 3²
It shows that 3 is to be used as a factor 2 times. (3 x 3), multiplied by itself and read as 3 squared or square of 3.
Example: When we write large numbers in short form, we use “Exponents.”
The expression 6 x 6 is written in a short form 6 x 6 = 6²
100000 = 10 x 10 x 10 x 10 x 10 = 105
105 stand for 10 x 10 x 10 x 10 x 10
“10” is called the base and “5” is exponent.
105 read as 10 to the power 5 or as simply fifth power of 10 or 10 to the fifth.
General form of Exponents
The base of an exponential expression can also be a letter or variable.
Exponentiation is a mathematical operation written as an involving two numbers base and the exponent or power.
Example: If a is a positive number and n is its exponent, then an means a is multiplied by itself n times.
The base a raised to the power of n is multiply a equal to the multiplication of a, n times.
an = a x a x a x …… x a n times.
= an means that a multiply by itself n times.
a is the base and n is the exponent.
an read as (i) “a raised to the nth power”, (ii) “a raised to the power of n”, (iii) “nth power of a”, (iv) ” a to be the nth power” or mostly as (v) “a to the nth”. where n is the integer.
Power: An expression that represents repeated multiplication of the same number is known as power.
Exponent: Exponent is the quantity that represents the power to which the number is raised.
An exponent is a positive or negative number, It is written as a small number to the right above to the base number., whose power we need to find.
Example: 105 here number 10 is known as base the number 5 is known as the exponent.
Example: When we write large numbers in short form, we use “Exponents.”
The expression 5 x 5 is written in a short form 5 x 5 = 5²
106 read as 10 to the power 6 or as simply sixth power of 10 or 10 to the sixth.
106 is called the exponential form of 1000000.
98 easy to read and write = 9 x 9 x 9 x 9 x 9 x 9 x 9 x 9
98 stand for = 9 x 9 x 9 x 9 x 9 x 9 x 9 x 9
“9” is called the base and “8” is exponent.
Now we will try to write 1000 in exponential form,
1000 = 10 x 10 x 10 = 103
10 is multiplied 3 times to 10
64 = 4 x 4 x 4
4 is multiplied 3 times to 4
“4” is called the base and “3” is exponent.
43 is called the exponential form of 64.
625 = 5 x 5 x 5 = 53
81 = 3 x 3 x 3 x 3 = 34
We can also writing this way when base is negative integer.
-24 = (-2) x (-2) x (-2) x (-2) = 16
-25 = (-2) x (-2) x (-2) x(-2) x (-2) = -32
-14 = (-1) x (-1) x (-1) x (-1) = 1
-13 = (-1) x (-1) x (-1) = -1
We see that in the expansion of (-13 and -25 ), we get, (-) sign, and in expansion of (-14 and -24 ), we get (+) sign.
Odd power is (-) sign, and even power is (+) sign, even number
(-1)Odd number = – 1
(-1)even number = + 1
How to solve negative exponents
The negative exponent of a number is equivalent to reciprocal of positive number.
a-n = 1/an
an = 1/a-n
Let’s understand the concept
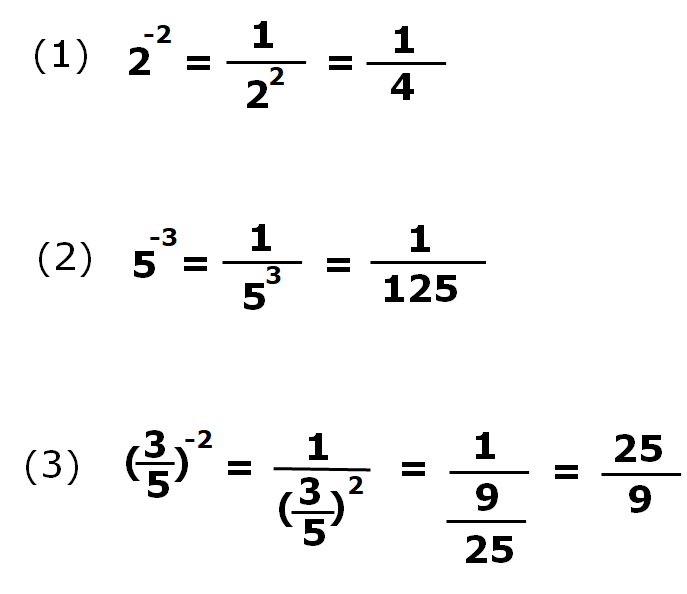
We also take any integer ‘a’ as a base in place of a fix number and write the number as
a²= a x a (a squared or a to the power 2)
a³ = a x a x a (a cubed or a to the power 3)
a4 = a x a x a x a (a to the power 4)
We see some examples
Express the following in exponential form
1. 7 x 7 x 7 x 7 x 7 x 7
7 multiply to 7, 6 times, so the exponential form is 76.
2. a x a x a x a x a x a x a x a
a multiply to a 8 times, so the exponential from is a8
3. b x b x b x b
b multiply to b 4 times, so the exponential form is b4