Simplification Fractions -Rule

What is Simplest Form form of a Fraction

The simplest form of a fraction, also known as the reduced form or lowest terms, is when the numerator (the top number) and the denominator (the bottom number) of the fraction have no common factors other than 1.

In other words, the fraction is simplified as much as possible.

Example: Fraction 3/7 is in the simplest form because 1 is the only common factor of 3 and 7.

Steps to Simplify a Fraction

1. Find the Greatest Common Divisor (GCD):
   • The GCD of two numbers is the largest number that divides both of them without leaving a remainder.
   • There are various methods to find the GCD, such as the Euclidean algorithm.
2. Divide the Numerator and Denominator by the GCD:
   • Once we have the GCD, divide both the numerator and the denominator by this number. The result will be the simplest form of the fraction.

Example

Consider the fraction 24/36.

1. Find the GCD of 24 and 36:
   • The divisors of 24 are 1, 2, 3, 4, 6, 8, 12, and 24.
   • The divisors of 36 are 1, 2, 3, 4, 6, 9, 12, 18, and 36.
   • The common divisors are 1, 2, 3, 4, 6, and 12.
   • The greatest common divisor is 12.
2. Divide the Numerator and Denominator by the GCD:

(24/36)÷12=(24÷12)/(36÷12)

=2/3.

So, the simplest form of 24/36 is 2/3.

Example: For 24 (2^3 * 3) and 36 (2^2 * 3^2), the common prime factors are 2 and 3. The GCD is 2²⋅3=4⋅3=12.

Why Simplify Fractions?

Ease of Understanding: Simplified fractions are easier to understand and work with, especially when performing arithmetic operations like addition, subtraction, multiplication, and division.

Standard Form: It is often required in mathematics to present answers in their simplest form.

Comparability: Simplified fractions make it easier to compare different fractions to see which is larger or smaller.

Methods to Find the GCD

1. Listing Common Factors:
   • List all factors of both the numerator and the denominator, then choose the greatest one that appears in both lists.
2. Prime Factorization:
   • Break down both numbers into their prime factors. Multiply the common prime factors to get the GCD.
   • Example: For 24 (2^3 * 3) and 36 (2^2 * 3^2), the common prime factors are 2 and 3.
   • The GCD is 2²⋅3=4⋅3=12.
3. Euclidean Algorithm:
   • This algorithm involves repeated division. For two numbers a and b, where a>ba > ba>b, the GCD is found by:
     • Dividing a by b and taking the remainder r.
     • Replacing a with b and b with r.
     • Repeating the process until the remainder is 0. The divisor at this step is the GCD.

Example Using Euclidean Algorithm

For 48/18:

1. Divide 48 by 18 to get a remainder of 12 (48 = 18 * 2 + 12).
2. Divide 18 by 12 to get a remainder of 6 (18 = 12 * 1 + 6).
3. Divide 12 by 6 to get a remainder of 0 (12 = 6 * 2 + 0).
4. Since the remainder is now 0, the GCD is 6.

Simplify the fraction by dividing both the numerator and the denominator by the GCD:

{(48/18)÷6}={(48÷6)/(18÷6)}=8/3​.

So, the simplest form of 48/18 is 8/3​.

Second Method:

How to Simplify Fractions

There are 2 methods to simplify fractions.

Method 1:

Simplify Fractions Step by Step

Step 1: Write the factors of numerator and denominator.

Step2: Identify common the factors of the numbers which are in numerator and denominator.

Step 3: In this step, we divide the numerator and denominator by common factors until they have no common factor other than 1.

So, the obtained fraction is in simplest form.

Let’s understand this method with the help of an example.

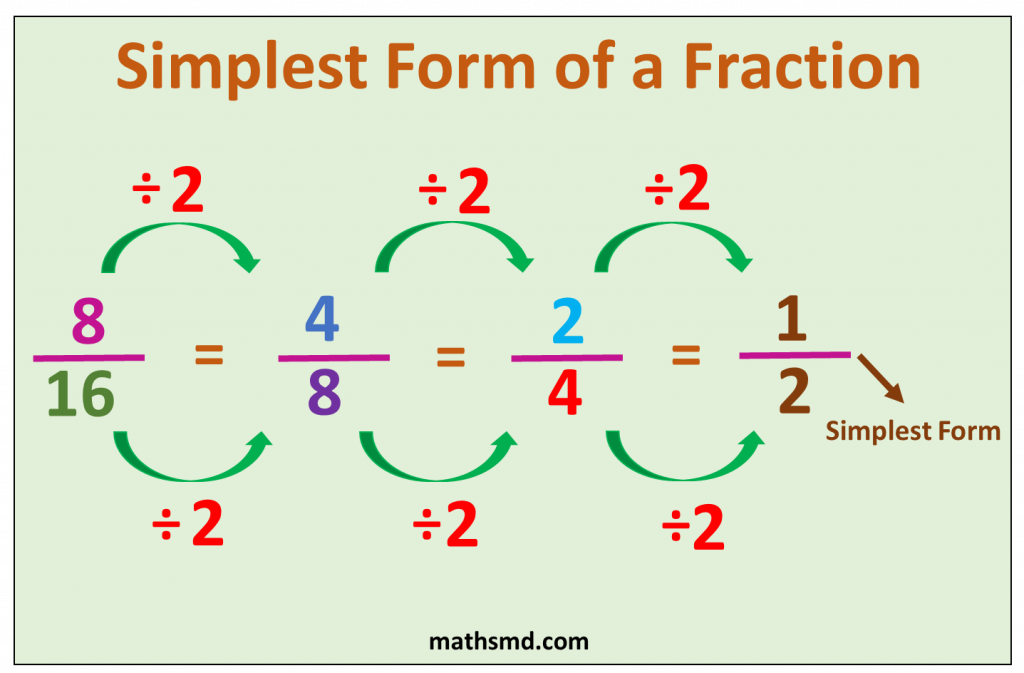
Write the fraction 8/16 in its simplest form.

Solution: Given fraction is 8/16.

Step1: Let us write factors of 8 and 16.

The factors of 8 and 16 are

Factors of 8: 1, 2, 4, and 8

Factors of 16: 1, 2, 4, 8 and 16

Step2 : Dividing the numerator and denominator by the common factors.

(8 ÷ 2 )/(16 ÷ 2) = 4/8

(4 ÷ 2 )/(8 ÷ 2) = 2/4

(2 ÷ 2 )/(4 ÷ 2) = 1/2

Thus, 1/2 is the simplified fraction of 8/16.

Method 2:

Step 1: Write the factors of numerator and denominator.

Step 2: Find the (HCF) highest common factor of the numerator and denominator.

Step 3: Divide the numerator and denominator by highest common factor(HCF).

Obtain fraction is in the simplest form.

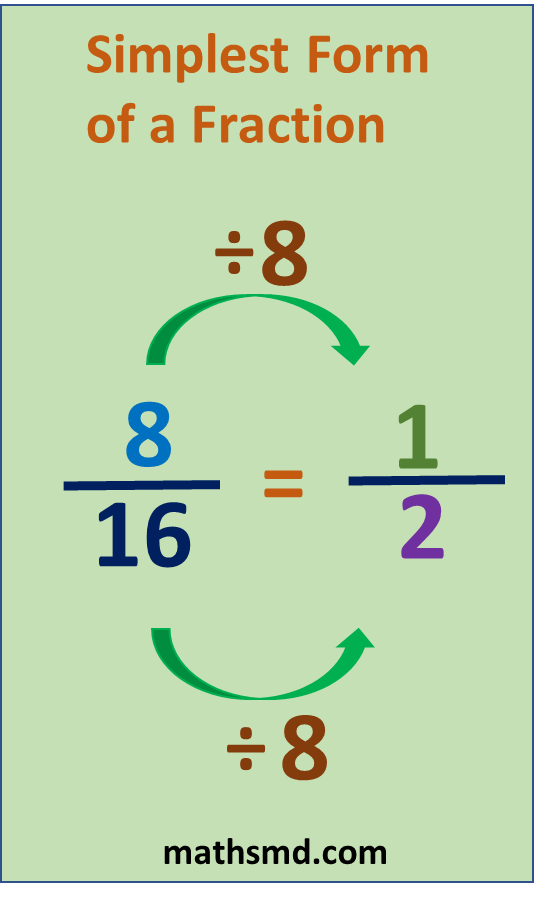
Let us simplify the fraction 8/16.

The highest common factor of 8 and 16 is 8.

Dividing both numerator 8 and denominator 16 by 8.

(8 ÷ 8)/(16 ÷ 8) = 1/2

We get simplest form of the fraction 8/16, that is 1/2.

So, the shortest way to solve a fraction into a simplest form is to divide the numerator and denominator by its highest common factor.

Example: The simplest form of 45/75

We see that both numerator(45) and denominator(75) is divisible by 3.

45/75 =  (3 x 15)/(3 x 25) = 15/25 

But 15 and 25 also have common factor other than 1.

15 and 25 both divisible by 5.

Now 3 and 5 have no common factor expect 1, we say that the fraction 3/5 is in the simplest form. 

Example: The simplest form of 48/60

We see that both numerator(48) and denominator(60) is divisible by 2.

48/60 = (2 x 24)/(2 x 30)=24/30

But 24 and 30 also have common factor other than 1.

24 and 30 both divisible by 2.

24/30 = (2 x 12)/(2 x 15)

Therefore, 24/30 = 12/15

12 and 15 also have common factor other than 1, that is 3.

12/15 = (3 x 4)/(3 x 5) = 4/5

Now 4 and 5 have no common factor expect 1, we say that the fraction 4/5 is in the simplest form. 

Note: The simplest form of a fraction is equivalent to the given fraction.

Understanding the simplest form of a fraction and the methods to simplify it is crucial for mathematical accuracy and efficiency.

Remember: A fraction is said to be in its simplest Form, if 1 is the only common factor of its numerator and denominator. or

If a fraction have no common factor except 1, in their numerator and denominator is said to be it’s “Simplest Form”.