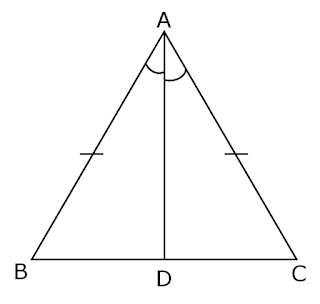
Theorem – Angles opposite to equal sides of an isosceles triangle are equal

Angles opposite to equal sides of an isosceles triangle are equal.

Given: A isosceles triangle △ ABC in which AB = AC, and
angles opposite to equal sides of triangle are ∠B and ∠C.

To prove: We need to prove that ∠B and ∠C, are equal
                           ∠B = ∠C.

Construction: Draw the bisector of ∠A, and let D be the point of intersection of this bisector.

Proof:  In △ ABD and △ACD

AB = AC  (Given)

AD =AD (Common)

 ∠BAD = ∠CAD (by construction)

△ ABD ≅  △ACD (by SAS rule)

Thus,  ∠ABD = ∠ACD (Angles are corresponding angles of congruent triangles) So, 

∠B = ∠C

                               Hence proved.

Related posts:

  1. Theorem – The line segment joining the mid-points of two sides of a triangle is parallel to the third side.
  2. The side opposite to equal angles of a triangle are equal
  3. Theorem – The perpendicular from the center of a circle to a chord bisects the chord
  4. Two triangles on the same base (or equal bases) and between the same parallels are equal in area
  5. Theorem – Alternate Interior Angles are Equal
  6. Two triangles having the same base(or equal bases) and equal areas lie between the same parallels
  7. Theorem – If the diagonals of a Quadrilateral bisect each other then that Quadrilateral is a Parallelogram
  8. (AA) Angle – Angle – Similarity – Theorem
  9. Theorem – If the angles subtended by the chords of a circle at the centre are equal, then the chords are equal
  10. The sum of the angles of a triangle is 180-Theorem

Leave a Reply

Your email address will not be published. Required fields are marked *