Two triangles on the same base (or equal bases) and between the same parallels are equal in area.

Given: △ ABC and △ PBC are two triangles on same base (or equal bases) BC and between the same parallels, BC and AP.

To prove: ar △ ABC = ar △ PBC

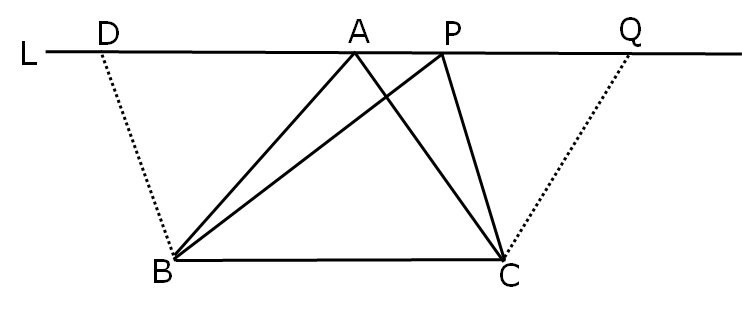
Construction: Through B, draw BD ∥ CA intersecting PA produced at D, and through C draw CQ ∥ BP intersecting BP produced at Q.

Poof: BCQP and ADBC are parallelograms (two pairs of opposite sides are parallel)

Also parallelogram BCQP and parallelogram ADBC are on the same base BC and same parallels BC and AP.

BCQP is a parallelogram with diagonal PC

Area of a triangle is half of a parallelogram, on the same base and between the same parallels.

ar(△PBC) = ar 1/2 (BCQP)……(1)

Again BCAD is also a Parallelogram with diagonal AB.

ar (△ABC) = ar 1/2 (ADBC)……(2)

Since parallelogram BCQP and parallelogram ADBC are on the same base BC and between the same parallel BC and DQ.

From eq.(i) and eq(2)

ar(∥gm BCQP) =ar(∥gm ADBC)

∴ ar(△PBC) = ar(△ABC)

ar (△ABC)= ar(△PBC)

Hence proved