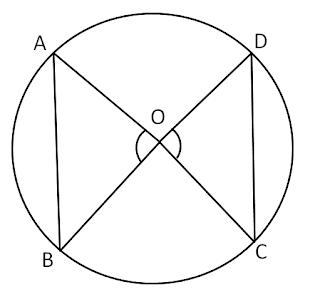
Theorem – Equal chords of a circle subtend equal angles at the center

Equal chords of a circle subtend equal angles at the center.

Given:  Two equal chords AB and CD of a circle with center O. i,e. AB = CD.

To prove: ∠AOB = ∠COD

Proof:  In △AOB and △ COD

OA = OC (Radius of circle)
OB = OD (Radius of circle)
AB = CD  (Given)

Hence, △AOB ≅ △ COD (SSS Congruence rule)

    ∴   ∠AOB = ∠COD (Corresponding parts of congruent triangles)

 Hence proved

Related posts:

  1. Theorem – If the angles subtended by the chords of a circle at the centre are equal, then the chords are equal
  2. Theorem – The perpendicular from the center of a circle to a chord bisects the chord
  3. Theorem – The perpendicular from the center of a circle to a chord bisects the chord
  4. Parts of a Circle – Definition, Examples and Formula – Radius – Diameter – Chord – Circumference – Arc – Area – Sector –
  5. Circle Worksheet
  6. Arc – Definition & Example – Arc length Formula – Geometry
  7. Cyclic Quadrilaterals: Definition, Properties, Examples
  8. Theorem – The line drawn through the center of a circle to bisect a chord is perpendicular to the chord
  9. In a parallelogram, opposite sides are equal
  10. Theorem – A diagonal of a parallelogram divides it into two congruent triangles

Leave a Reply

Your email address will not be published. Required fields are marked *