Volume of Right Circular Cone 

                       

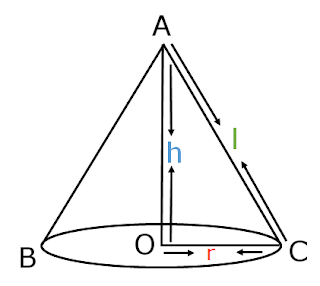
In figure A is called vertex, AO is height,  OC is radius, and AC is slant height of cone.

The height, radius, and slant height of the cone are usually denoted by h, r and l respectively.

Volume of Right Circular Cone V = 1/3𝜋r²h

Where V =  Volume of Right Circular Cone,
           r = Radius of circular base,
    and h = height of cone.

            V = 1/3 x area of base x height

The unit of volume will be cubic unit e.g. m³, cm³, etc.

(1)  l² = r² + h²

Here h is height of cone so by applying Pythagorean theorem,
                         l = √r² + h²

There are some steps to find volume of right circular cone.

Step 1:                    Radius 

When in the question given diameter, we will find radius with the help of formula,    

Diameter = 2 x Radius

Radius of the circular base is generally given in the question. 

Step 2:                   Height

Height of the right circular cone is either given or can be calculated if slant height is given in the question.

This can be done applying Pythagorean theorem. 

 l = √r² + h²

Here, l represents slant height, r and h stand for radius and height.

Step 3 : Substitute the values of height and radius in the formula of volume                            

 V =1/3𝜋r²h

Step 4 : Calculate and find the volume. Represent it with units e.g., m³, cm³, etc.

Example Problems with solutions 

(1) The height and slant height of a cone are 4 cm and 25 cm respectively. Find the volume of the cone.

Solution : Here height h = 4 cm, and slant height l = 25 cm

l = √r² + h²

25 = √r² + 4²

25 = √r² + 16

25 – 16 = √r² 

9 = r²

 r = 3 cm

So, Volume of cone V = 1/3𝜋r²h 

                              = 1/3 x 22/7 x 3 x 3                   

            = 66/7 cm³

       Volume of cone V = 9.4 cm³