Associative Property of Rational Numbers
Associative Property of Rational Numbers
Associative Property
Associative property of rational numbers states that when three or more rational numbers are added or multiplied the result remains same irrespective of how they are grouped.
However, in the case of subtraction and division if the order of the numbers is changed then result will also change.
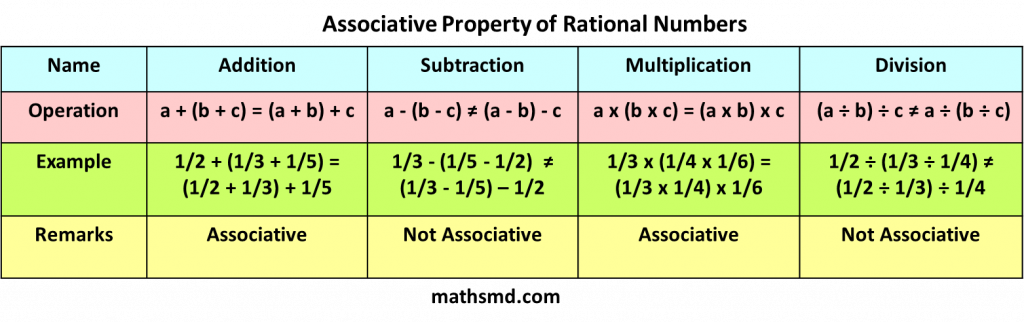
we will understand this property on each operation using examples.
Associative Property for Addition
Associative property for addition of rational numbers states that sum of three or more rational numbers does not depend on the way the rational numbers are grouped, i.e.,
if a, b, c are three rational numbers then the sum of rational numbers is also a rational number.

For any three rational numbers, associative property for addition is expressed as
(a + b) + c = a + (b + c)
Example: (1/2 + 1/3) + 1/4
= (3 + 2)/6 + 1/4
= 5/6 + 1/4
= (20 + 6)/24
= 26 /24
= 13/12
1/2 + (1/3 + 1/4)
= 1/2 + (4 + 3)/12
= 1/2 + 7/12
= (6 + 7)/12
= 13 /12
13/12 = 13/12
When any three rational numbers are added the result remains the same.
We say that addition is associative for rational numbers.
Associative Property for Subtraction
For any three rational numbers, associative property for subtraction is expressed as
(a – b) – c ≠ a – (b – c)

Example: (1/2 – 1/3) – 1/4 ≠ 1/2 – (1/3 – 1/4)
We say that subtraction is not associative for rational numbers.
Associative Property for Multiplication
For any three rational numbers, associative property for multiplication is expressed as, i.e., if a, b, c are three rational numbers then
(a x b) x c = a x (b x c)

Example: (1/5 x 1/6) x 1/4 = 1/120
1/5 x (1/6 x 1/4) = 1/120
(1/5 x 1/6) x 1/4 = 1/5 x (1/6 x 1/4) = 1/120
When any three rational numbers are multiplied the result remains the same.
We can say that multiplication is associative for rational numbers.
Associative Property for Division
For any three rational numbers a b and c, associative property for division is expressed as
(a ÷ b) ÷ c ≠ a ÷ (b ÷ c)

Example: Solve (2/3 ÷ 1/2) ÷ 3/4 and 2/3 ÷ (1/2 ÷ 3/4)
(2/3 ÷ 1/2) ÷ 3/4
= (2/3 x 2/1) ÷ 3/4
=(2 x 2)/(3 x 1) =
4/3 ÷ 3/4
= 4/3 x 4/3
= (4 x4)/(3 x 3)
= 16/9
2/3 ÷ (1/2 ÷ 3/4)
= 2/3 ÷ (1/2 x 4/3)
= 2/3 ÷ 4/6
= 2/3 x 6/4
= (2 x 6)/(3 x 4)
= 12/12
= 1
16/9 ≠ 1
We can say that the expressions on both sides are not equal.
So division is not associative for rational numbers.